就職活動に欠かせない一般常識筆記試験。企業によって違いもありますが、多くは一般常識とSPI3の両方が課されます。国家試験や就職活動に関するテキストを作り続けているウイネットが培った知見をもとに、学生がつまずきやすい分野を分析。

その中でもとくに苦手意識が高いと言われる、数学分野の対策をご紹介します。

※本記事の内容は書籍「専門学校生のための就職筆記試験対策問題集」（ウイネット）を再編集したものです。

数学の解き方は「パターンの理解」がキモ！

就職筆記試験での数学の問題は、解き方を知ってさえいればさほど難しくなく正答を出すことができます。つまり「パターンの理解」が重要です。

今回は、SPI3でもよく出題される「旅人算」を例に解き方をご紹介します。

旅人算とは？

2人以上の人が移動している中で、両者間の距離や出会うまでの時間などを計算する方法です。例えば、「違う地点から出発したAとBが合流するまで何分かかるか」といった問題です。

・両者が同じ方向へ進むパターン

Bが先に進むAを追いかける場合は、両者の速さの差で考えます。

・両者が反対方向に進むパターン

違う方向からやってきたAとBが出会う場合は、両者の速さの和で考えます。

例題を解いてみよう

例題1

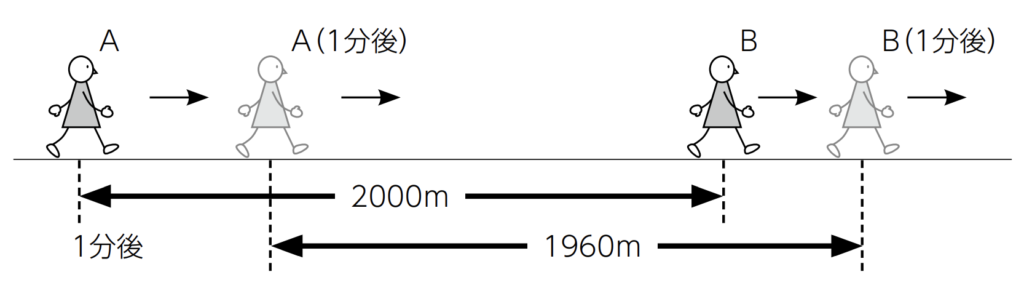
2km離れた地点から、AがBを追いかけます。Aが時速6km、Bが分速60mだとすると、AがBに追いつくのは何分後でしょうか。

ポイント
・両者の速度の差で計算する
・単位が時速と分速で異なるため、そろえてから計算する

解き方
①解答の単位は「分」なので、両者の速度を分速にそろえます。
A：（6×1000）÷60 ＝100m/分
B：60m/分

②100（Aの分速）-60（Bの分速）＝40m/分
ここから、Aは1分につき40mずつBに近づくことがわかります。

③2km＝2000m÷40m＝50（分）
解答：50分後

例題2

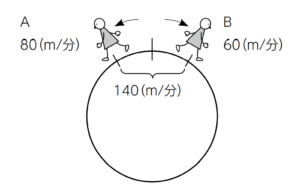
ある池の周りを、Aは分速80mで、Bは分速60mで歩いています。2人が反対方向に向かっている場合、AとBが30分ごとに出会うとすると、池の周りは何mあるでしょうか。

ポイント
・両者の速度の和で計算する

解き方
①AとBが一度出会ってから、次に出会うまでに2人が進んだ距離の和が池の周囲の長さとなる。

② 80（Aの分速）＋60（Bの分速）＝140m/分
1分に140mずつ進んでいることがわかる。

③2人は30分後に出会うため、140（1分に進む距離の和）×30（分）＝4200（m）
解答：4200m

数学の学習は、論理的な思考の訓練になる

社会人生活の中で、実際にこのままの計算式を使う機会はそう多くはないかもしれません。しかし数学的な考え方は、学生が社会に出たときに、他人に自分の意思を正しく伝える際に役立ちます。

数学的な考え方とは、論理立てて考える思考、いわゆる「ロジカルシンキング」。これを身につけるために、数学の学習は最適な訓練だと言えるでしょう。

本書籍には、数学以外にも就職筆記試験に役立つ問題を豊富に掲載しています。ぜひご活用ください。

この記事を書いた人

株式会社ウイネット

ウイナレッジを運営している出版社。
全国の専門学校、大学、職業訓練校、PCスクール等教育機関向けに教材を制作・販売しています。