
連載学生の「数学嫌い」を克服!つまずき解消ピンポイント解説&演習
基礎学力分野の中でも特に苦手意識を持つ学生の多い「数学・算数」。この連載では、小学校算数まで立ち返り「学生がどこでつまずいたのか」「どうすれば克服できるのか」を解説!各回には「学生に配布可能な練習プリント(PDF)」もついています。ぜひ学生の苦手克服にお役立てください。
学生が「算数・数学嫌い」になってしまう原因の一つは、算数・数学が「積み上げ型学習」であること。
前の単元の上に新しい単元の知識を積み上げていく学習では、学習していて一度わからなくなると、そのあともあちこちでほころびが出てしまいます。
まずはどこでつまずいているのかはっきりとさせ、コツコツとそのほころびを修復し、軌道をもとに戻していくことが大切です。
本シリーズでは、数学に苦手意識のある専門学校の学生さんが、小学校~高校までで「つまずいた」であろう単元を簡単にサクッとわかりやすく解説します。
さらに記事に付属の「練習プリント」をお使いいただくことで、学生さんのつまずきをスッキリ解消&苦手意識を克服していただけます。
第4回となる今回のテーマは「割合」です。

目次
割合の基礎
前回までの記事でも確認しましたが、積み上げ型学習である算数・数学の根底にあるのはやはり四則演算です。
身につけたことを応用できるよう徐々にグレードアップしていきましょう。
今回は、「割合」を取り上げます。
「割合」は、小学校算数のつまずきポイントの第4関門です。
どのような点につまずくことが多いのでしょうか。それぞれを順番に見ていきましょう。
単位換算の思考ポイントとは? とっつきやすく考えるには
「割合」の計算のつまずきポイントは、以下の3つです。
1. 割合の式の成り立ちが理解できていない
2. 問題に合わせて公式が活用できない
3. 単位換算が苦手
割合は「数えるための数」から「比べるための数」への概念の変換が必要なため、つまずいていることが多いです。
百分率の「パーセント」という表し方は日常生活の中で頻繁に目にします。
バーゲンセールに行けば、「全品10%OFF」といった表記を目にしたり、「今だけ10%増量!」という表記につられて買い物をしたりなど、一度は目にしたことがある概念だと思います。
百分率のルールは複雑ではなく、単純に百分のいくつかということを数字で表しただけなのですが、なぜつまずいてしまうのでしょうか。
もともとのわり算の概念が苦手な学生もいますので、その場合は、本連載の第2回「わり算(3ケタ÷2ケタ)」をしっかりと復習することをおすすめします。
対処法としては、身近な例の例題を用いて公式を使うところからはじめ、公式に合わせてドリルを解く、頭の中で単位換算、と少しずつステップアップをしていくといいでしょう。
また、かけ算、わり算を含めた四則演算も駆使しますので、四則演算に苦手意識のある学生は総合的な計算力を鍛えるのも重要です。
焦らずに基礎力を積み上げましょう。
基本的な計算式について
割合の第一公式: 割合 = くらべる量 ÷ もとにする量
割合の第二公式: くらべる量 = もとにする量 × 割合
割合の第三公式: もとにする量 = くらべる量 ÷ 割合
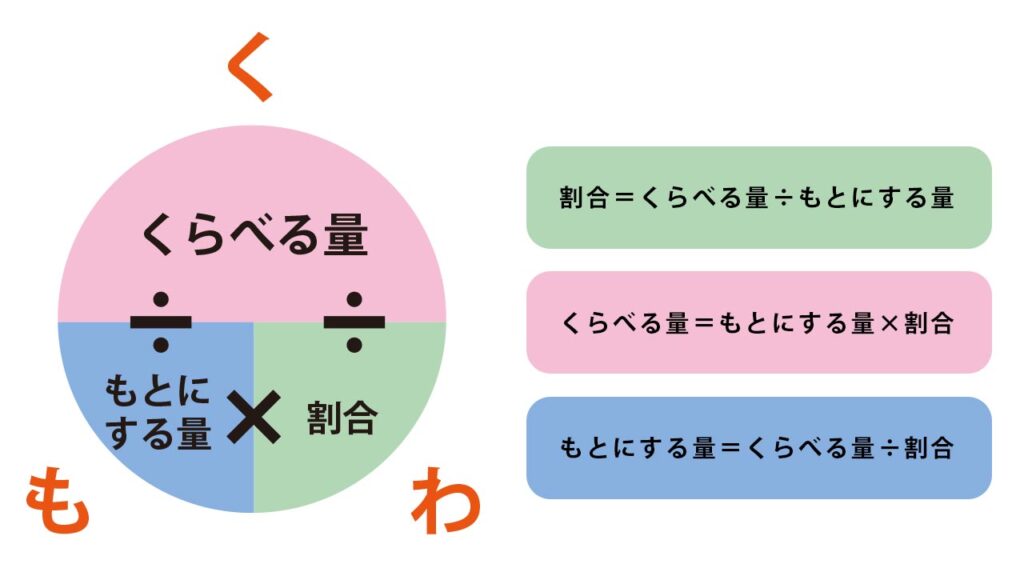
「くもわ」の公式とも言われていますが、公式を覚えるだけでは、計算はできても応用はできません。
以下のポイントを押さえて、概念を理解し、活用できるようにしましょう。
<ポイント>
割合を表すことば(歩合や百分率など)は、すべて「~倍」という意味である。
計算ドリルを解く際など、以下の表のようなものを見やすいところに置いて確認しながら解きましょう。
| 数 | 分数 | 百分率 | 歩合 |
|---|---|---|---|
| 1 | $$\frac{1}{1}$$ | 100% | 10割 |
| 0.1 | $$\frac{1}{10}$$ | 10% | 1割 |
| 0.01 | $$\frac{2}{100}$$ | 1% | 1分 |
| 0.001 | $$\frac{1}{1000}$$ | 0.1% | 1厘 |
| 0.123 | $$\frac{123}{1000}$$ | 12.3% | 1割2分3厘 |
| 1.6 | $$\frac{8}{5}$$ | 160% | 16割 |
繰り返し練習するうちに自然と概念が身についてきます。
以下の例を見てみましょう。


200gの30%増しの量を考えよう
では、次に実際に買い物のときによくある、30%増しや30%引きの計算を見てみましょう。
“200gの30%増し”というのは“200gに、200gの30%にあたる量を加える”という意味なので、
$$200+200×\frac{3}{10}=200+60=260(g) $$
になります。
また、この260gは、もとの量の200gの何倍になったものかを求めてみると、
$$260÷200=\frac{13}{10}(倍) \Rightarrow 1+\frac{3}{10} (倍)$$
よって、この量は、
$$200×(1+\frac{3}{10})= 260(g)$$
という考え方でも求められます。
このように“○増し”を“○倍”におきかえて 考える方が立式しやすいことが多いので、 マスターしておきましょう!

200円の30%引きの金額を考えよう
“200円の30%引き”というのは“200円から、200円の30%にあたる金額を値引きする”という意味なので、
$$200-200×\frac{3}{10}=200-60=140(円)$$
また、この140円は、もとの金額の200円の何倍になったものかを求めてみると、
$$140÷200=\frac{7}{10} (倍)\Rightarrow 1- \frac{3}{10}(倍) $$
です。
よって、この金額は、
$$200×(1-\frac{3}{10} )=140(円)$$
で求められます。
“〇引き”も“〇倍”におきかえて考える方が便利です。こちらもマスターしよう!

例にあげた割合の計算については、「myトレーニング」内で、動画付きの解説をしていますので、学生へのご指導にもお役立てください。
myトレーニング「割合①~基本~」動画サンプル

練習プリントDL
割合の計算練習ができるプリントをご用意しました。
こちらのPDFファイルは、
- 印刷して学生に配布
- 学内学習支援ツールへのアップロード・ファイル共有
等の形でご利用いただけます。
不特定多数の方が閲覧可能な形でのアップロード・再配布はご遠慮ください。
学生の皆さんのつまずき解消にぜひお役立てください。
\ぜひ投票お願いします/
真南風文藝工房 代表
ライター・サイエンスコミュニケーター
工学修士(航空宇宙学)
自動車メーカーでの先行開発エンジニアを経験した後、理系教材編集(小中高理科テスト編集・高校数学・中学校理科教科書編集)職に転向。
近年は環境・航空・宇宙・自動車・理科・数学・サイエンスなどを中心に幅広い分野での執筆活動にも取り組んでいる。



















