
連載学生の「数学嫌い」を克服!つまずき解消ピンポイント解説&演習
基礎学力分野の中でも特に苦手意識を持つ学生の多い「数学・算数」。この連載では、小学校算数まで立ち返り「学生がどこでつまずいたのか」「どうすれば克服できるのか」を解説!各回には「学生に配布可能な練習プリント(PDF)」もついています。ぜひ学生の苦手克服にお役立てください。
学生が「算数・数学嫌い」になってしまう原因の一つは、算数・数学が「積み上げ型学習」であること。
前の単元の上に新しい単元の知識を積み上げていく学習では、学習していて一度わからなくなると、そのあともあちこちでほころびが出てしまいます。
まずはどこでつまずいているのかはっきりとさせ、コツコツとそのほころびを修復し、軌道をもとに戻していくことが大切です。
本シリーズでは、数学に苦手意識のある専門学校の学生さんが、小学校~高校までで「つまずいた」であろう単元を簡単にサクッとわかりやすく解説します。
さらに記事に付属の「練習プリント」をお使いいただくことで、学生さんのつまずきをスッキリ解消&苦手意識を克服していただけます。
最終回となる第5回のテーマは、「面積・体積」です。

目次
面積・体積の基礎
前回までの記事で確認しましたが、積み上げ型学習である算数・数学の根底にあるのはやはり四則演算です。
今回も四則演算に触れますが、図形分野からのアプローチを試みます。
「面積・体積」は、小学校算数のつまずきポイントの第5関門です。
どのような点につまずくことが多いのでしょうか。それぞれを順番に見ていきましょう。
「面積・体積」のつまずきポイント
「面積・体積」のつまずきポイントは、以下の3つです。
1. 長方形の面積を求める公式から三角形の面積が求められることや角柱・角錐の体積の公式の関係などを概念的に理解していない
2. 公式の暗記になっていて、本番で計算ができない
3. 平面図形や立体図形が頭の中でイメージできない
③は、さまざまな図形に触れて練習あるのみ!です。
今回は①と②のつまずきポイントを克服しましょう。
まず、この①と②のつまずきの原因として、①の面積や体積の公式が理解できないから②のように暗記にたよってしまい、うろ覚えでいざテストなどの本番に臨むと、間違えてしまうといった悪循環に陥っていると考えられます。
長方形の面積を求める公式が<縦×横>で、三角形はその半分であることや、角柱・角錐の面積の公式の関係などについて図解を用いてイメージすることが重要です。
かけ算、わり算を含めた四則演算も駆使しますので、四則演算に苦手意識のある学生は総合的な計算力を鍛えるのも重要です。
焦らずに基礎力を積み上げましょう。
三角形の面積の求め方の公式について
いきなりですが、例題です。
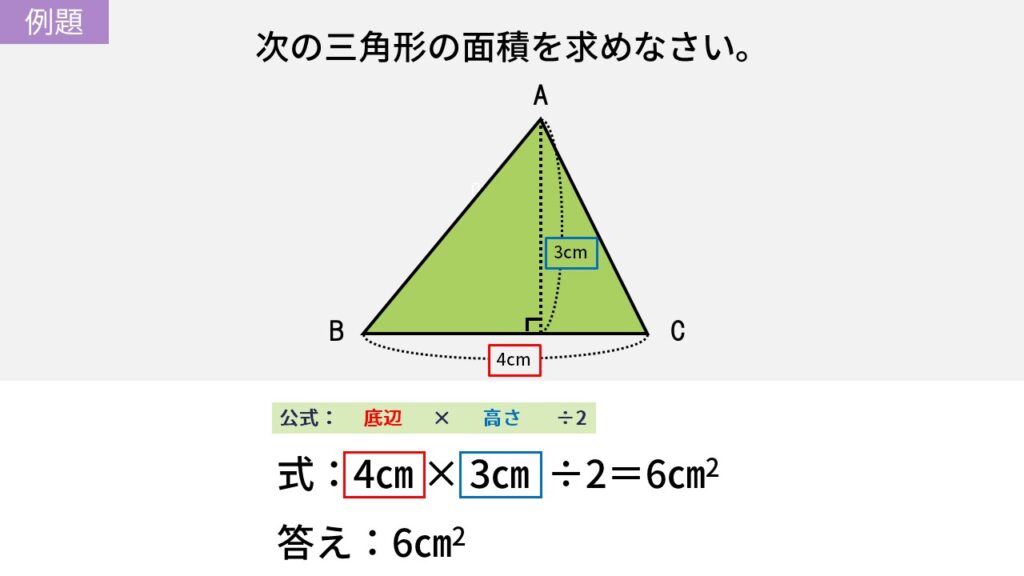
このとき使った、三角形の面積を求める公式の 「÷2」にはどのような意味があるのか、考えたことはあるでしょうか。
次の図のように、例題の三角形の図にマス目を書いて、赤と青の補助線を引いてみましょう。
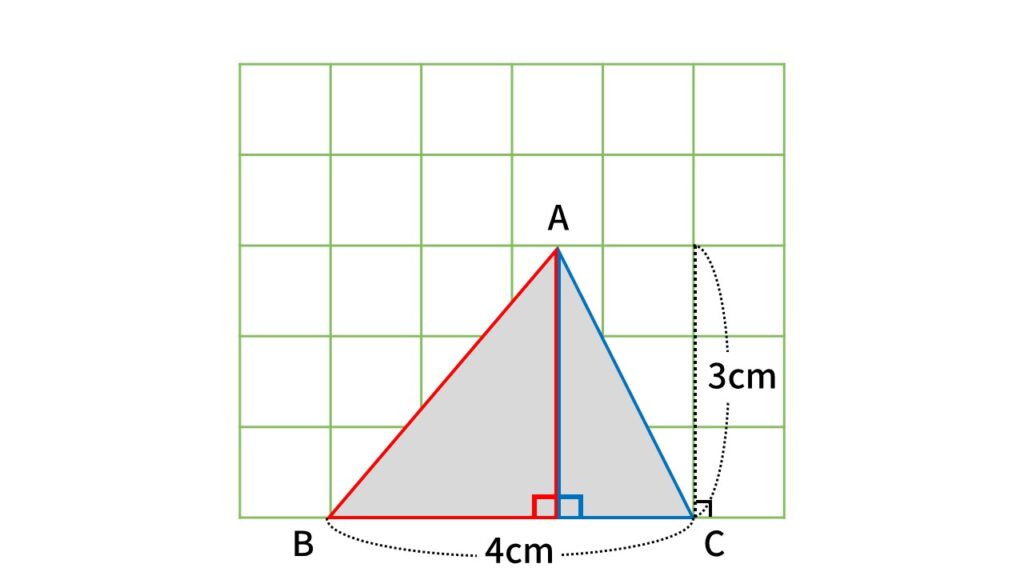
つぎに、赤い直角三角形をひっくり返して、外側に同じ形の直角三角形を書きます。
同様に、青い直角三角形をひっくり返して、外側に同じ形の直角三角形を書きます。
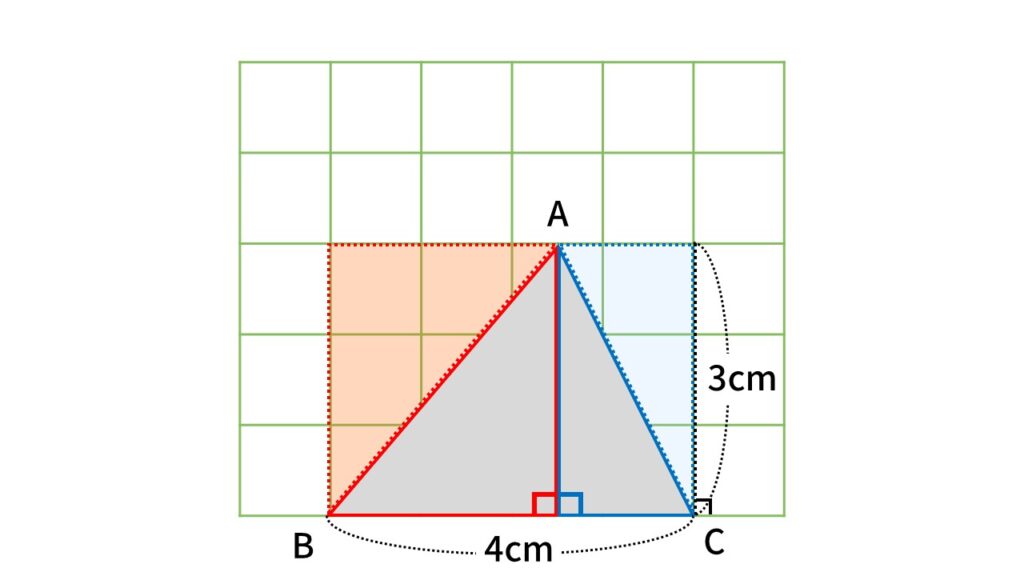
(縦)3㎝×(横)4㎝の長方形ができました。
長方形の面積は、三角形の面積2つ分ということがわかります。
それぞれの面積を求める公式は以下のとおりです。
長方形:縦×横
三角形:底辺(横)×高さ(縦)÷2
いかがでしょうか。
三角形の面積を求める公式は、<長方形の面積を求める公式÷2>になる理由が理解できましたか。
この例では、
長方形の面積:3㎝×4㎝=12㎠
三角形の面積:4㎝×3㎝÷2=6㎠
となります。
このように三角形の公式の成り立ち理解することで、もし公式を忘れても簡単に求めることができるようになります。
ポイント
左右の直角三角形を足して長方形を考える
三角錐の体積の求め方の公式について
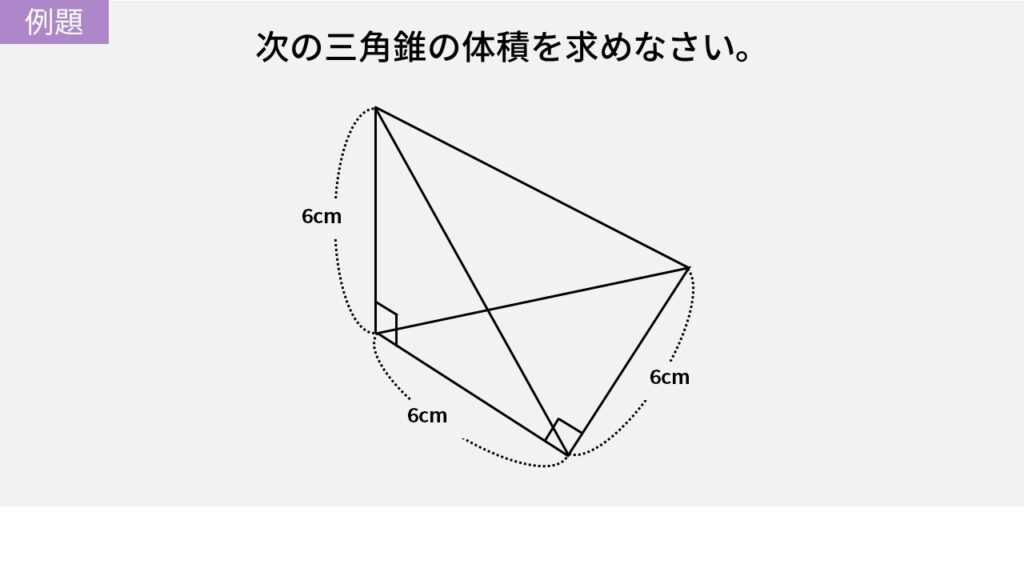
この問題は次の図のように考えます。
同じ三角錐を3つ用意し、これをうまく組み合わせてみましょう。
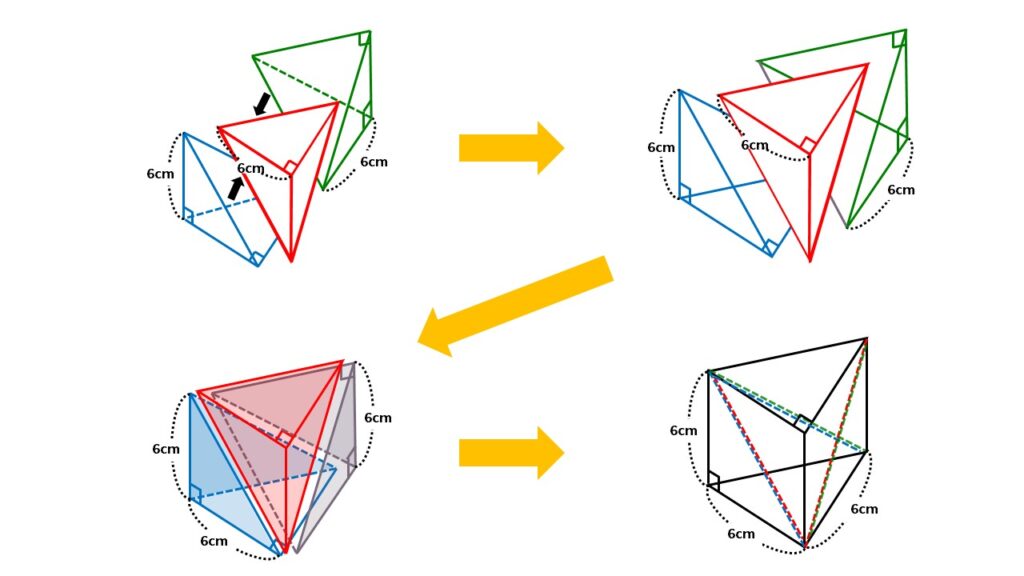
このように、三角柱になりました。
このことから、三角柱の体積は、三角錐の体積3つ分ということがわかります。
それぞれの体積を求める公式は以下のとおりです。
三角柱:底面積×高さ
三角錐:底面積×高さ÷3
底面積は、さきほどお伝えした三角形の面積の公式を使用して計算します。
この例題の答えは、
底面積:6㎝×6㎝÷2=18㎠
↓
三角柱の体積:18㎠×6㎝=108㎤
↓
三角錐の体積:108㎤÷3=36㎤
と求められます。
myトレーニングでは、いろいろな図形の面積や体積の動画解説をしています。学生のつまずきにあわせて適宜ご利用ください。
myトレーニング「いろいろな図形の面積①~基本~」動画サンプル

練習プリントDL
面積・体積の計算練習ができるプリントをご用意しました。
こちらのPDFファイルは、
- 印刷して学生に配布
- 学内学習支援ツールへのアップロード・ファイル共有
等の形でご利用いただけます。
不特定多数の方が閲覧可能な形でのアップロード・再配布はご遠慮ください。
学生の皆さんのつまずき解消にぜひお役立てください。
\ぜひ投票お願いします/
真南風文藝工房 代表
ライター・サイエンスコミュニケーター
工学修士(航空宇宙学)
自動車メーカーでの先行開発エンジニアを経験した後、理系教材編集(小中高理科テスト編集・高校数学・中学校理科教科書編集)職に転向。
近年は環境・航空・宇宙・自動車・理科・数学・サイエンスなどを中心に幅広い分野での執筆活動にも取り組んでいる。



















